Saturn and Kepler's Third Law

You should know that Kepler's Third Law relates the distance a satellite is from its parent body to the time taken for it to orbit. This applies to the planets orbiting the Sun, but can equally apply to artificial satellites (and the Moon!) orbiting the Earth, or other planets' moons in orbit.

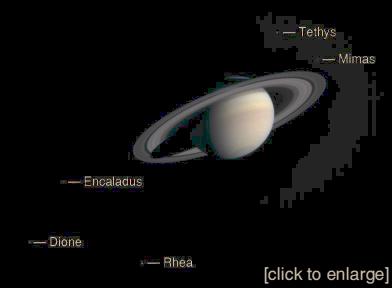
The image below shows Saturn and five of its moons. This was taken by the Cassini probe en route to Saturn on 5 December 2003. It is due to arrive on 1 July 2004. More info.

Question

1. Using the information in the table, show that the five moons obey Kepler's Third Law:

   Satellite	Average Distance from Saturn (103 km)	Time taken to orbit Saturn (h)
   Mimas	186	22·62
   Enceladus	238	32·88
   Tethys	295	45·31
   Dione	377	65·69
   Rhea	527	108·4

2. Plot a graph of T² against d³ and determine the proportionality constant for the Saturnian system. Don't forget that it has units!

3. Using your constant, predict:
   1. the orbital period of Titan, Saturn's largest moon (set to receive the European Space Agency's Huygens lander from Cassini) with an average distance of 1,222 × 10³ km.
   2. the average distance of Phoebe, a moon with a retrograde orbit that it takes 1.51 years to complete.

Hints

1. Recall that T²=kd³
2. Don't forget to use the correct powers of ten in determining your gradient
3. Be careful of the units used, especially part b!